中心陈基课题组与智能学院王立威贺笛课题组、字节跳动研究部门合作，使用深度学习技术求解薛定谔方程取得重要进展。在这项工作中，研究团队针对基于神经网络的量子变分蒙特卡洛算法（NNVMC），设计了全新的高效计算框架“Forward Laplacian”和相匹配的高效神经网络模型LapNet。所提出的方案在完全不损失计算精度的前提下为NNVMC方法带来了十倍以上的加速，显著地扩展了该方法的适用范围，并为其它精确计算方法提供了宝贵的参考。相关研究成果以“A computational framework for neural network-based variational Monte Carlo with Forward Laplacian”为题，于2024年2月13日发表在《自然-机器智能》（Nature Machine Intelligence）。

文章截图

在量子化学领域，一个重要的问题是如何数值求解多电子体系薛定谔方程，从而推定基态能量、体系电极性等重要的物理化学性质。近年，NNVMC借助深度学习模型的强大表达能力在这一问题上取得突破性进展，大幅提升了从头计算(ab initio)方法对于基态能量的计算精度，因此受到计算化学家的广泛关注。然而，其高额的计算成本限制了该方法在实际场景中的应用。

为提升NNVMC的计算效率，研究团队提出了全新的计算框架“Forward Laplacian”。该框架针对NNVMC的瓶颈，创造性地利用前向传播优化了计算流程。该改进使得计算效率提升显著，并有效扩大了算法所适用的体系规模。

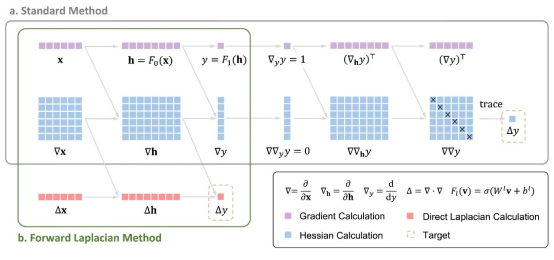
Forward Laplacian计算框架对比原有方法显著削减计算开销

研究团队进一步从Forward Laplacian框架能利用梯度计算的稀疏性这一特性出发，设计了神经网络模型LapNet。LapNet在保证计算精度的同时，增加了梯度计算的稀疏性，从而获得进一步的加速。

两者的有机结合使得新算法的计算效率显著高于相关领域的代表性工作FermiNet、PauliNet2、Psiformer。由于算法所适用的体系规模已经显著扩大，研究团队进而测试具备充分物理、化学意义，但此前对NNVMC而言极具挑战性的过渡金属电离能、反应能垒、解离能等相对能量计算任务，并取得了理想的结果。

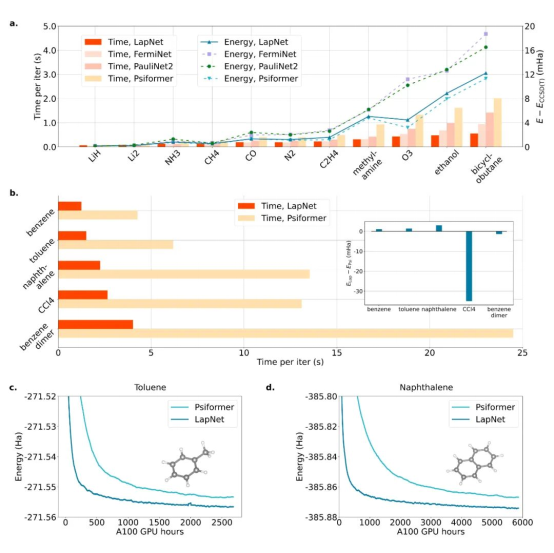
LapNet相对FermiNet、PauliNet2、Psiformer，在若干分子体系上显著提升精度

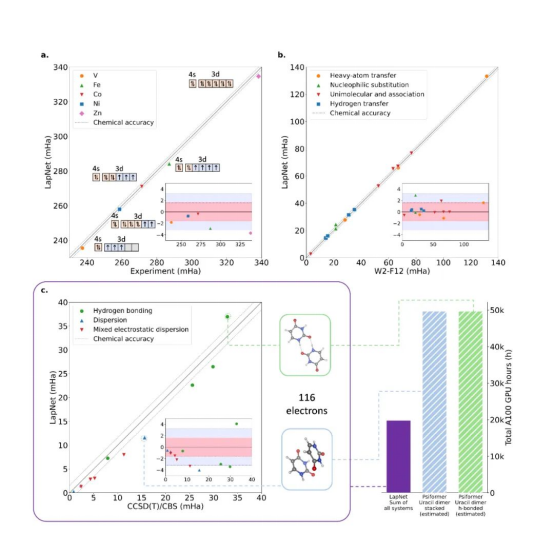
LapNet在相对能量计算中的表现

该研究显著优化了NNVMC的计算效率，扩展了算法所适用的体系规模，展现了深度学习方法应用于量子力学问题的巨大潜力。该工作已受到相关研究人员的广泛关注，有望促进深度学习在更一般的科学问题中的应用。

北京大学智能学院王立威教授、北京大学物理学院陈基助理教授、北京大学智能学院贺笛助理教授、字节跳动研究部任维络博士为该论文的共同通讯作者，北京大学智能学院博士研究生李瑞晨、北京大学元培学院本科毕业生叶皓天（现为斯坦福大学博士研究生）为该论文的共同第一作者。该工作得到了国家自然科学基金委和科技部的资助。